Page 84 - 无损检测2023年第八期

徐晓阳, 等:

基于声发射信号能量衰减的混凝土材料损伤检测

生宏观裂纹时期, 此期间, 大量位置相近、 模态相同 凝土材料内以线性路径传播至两个传感器, 且局部可
的源信号发生叠加, 传感器采集到数个能量值超过 能存在“ 混凝土 - 钢筋 - 混凝土” 的复合传播路径。

5000的信号, 故累计能量陡升。第二段对应试件 ( 3 ) 破坏阶段: 试件失效破坏产生的声发射信号
发生脆性破坏时期, 此期间, 各种裂纹同时产生, 源 密集且能量值跨度大, 成对信号能量衰减相对比率相
信号产生位置离散且模态各异, 传感器采集到大量 差较大。该阶段可对应图8衰减系数曲线最后一个

密集的能量值超过200的信号, 所以累计能量上升 数据点, 衰减系数平均值为5.698×10 mm 。
-3
-1
幅度和速率均较大。 3.4 能量衰减与损伤演变的关联模式
通过累计能量曲线可以发现, 传感器 A1 采集 由于试件产生宏观裂纹后, 声发射弹性波以非
到的信号总能量大于 A2 采集到的, 这与之前计算 线性混合路径进行传播, 能量衰减模型在机理上不

采集相对能力ln ( C 1 C 2 > 0 相对应, 故传感器 再适用, 故文章将重点分析试件在未裂阶段的能量
/ )
A1采集能力稍强于 A2 。 衰减系数。为便于分析, 对试件 Z1 , Z2 , Z3 在该阶
3.3 衰减系数B 的计算 段所受荷载进行归一化, 利用施荷应力水平来研究
波速衰减模型确定后, 可计算得到单个源信号 损伤和能量衰减系数的关联模式, 得到结果如图 9
被两个传感器以最快模式采集到的最大时差为 所示。
0.388×10 s 。每次加载后, 需筛选出时差满足要
-3
求, 能量相近的成对信号对衰减系数进行计算。随
着荷载增加, 试件损伤逐渐增加, 采集到的声发射信
号变得更加密集。为便于计算, 在单次加载产生的
成对信号中, 每连续30对信号进行一次计算, 得到
多个能量衰减系数, 取其平均值, 由此可以得到加载
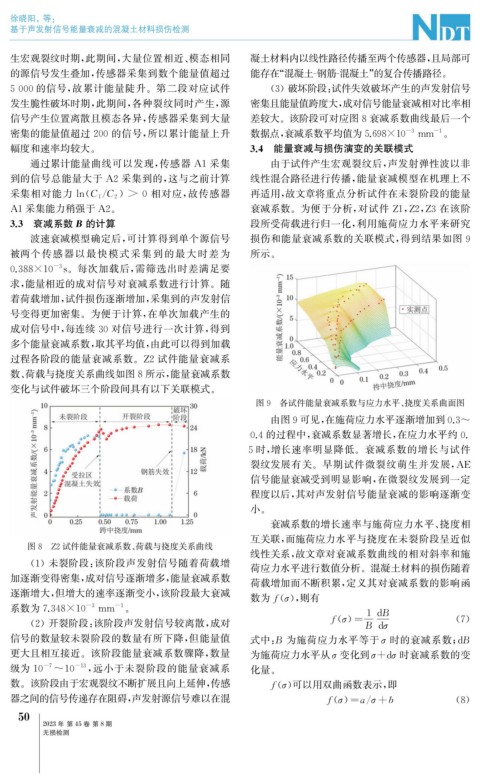
过程各阶段的能量衰减系数。 Z2 试件能量衰减系
数、 荷载与挠度关系曲线如图8所示, 能量衰减系数
变化与试件破坏三个阶段间具有以下关联模式。
图9 各试件能量衰减系数与应力水平、 挠度关系曲面图

由图9可见, 在施荷应力水平逐渐增加到0.3~
0.4的过程中, 衰减系数显著增长, 在应力水平约0.
5时, 增长速率明显降低。衰减系数的增长与试件

裂纹发展有关。早期试件微裂纹萌生并发展, AE
信号能量衰减受到明显影响, 在微裂纹发展到一定
程度以后, 其对声发射信号能量衰减的影响逐渐变
小。
衰减系数的增长速率与施荷应力水平、 挠度相
互关联, 而施荷应力水平与挠度在未裂阶段呈近似
图8 Z2试件能量衰减系数、 荷载与挠度关系曲线
线性关系, 故文章对衰减系数曲线的相对斜率和施

( 1 )未裂阶段: 该阶段声发射信号随着荷载增
荷应力水平进行数值分析。混凝土材料的损伤随着
加逐渐变得密集, 成对信号逐渐增多, 能量衰减系数
荷载增加而不断积累, 定义其对衰减系数的影响函
逐渐增大, 但增大的速率逐渐变小, 该阶段最大衰减
数为 ( σ ), 则有
f
-1
-3
系数为7.348×10 mm 。 1dB
()

( 2 )开裂阶段: 该阶段声发射信号较离散, 成对 fσ = B dσ ( 7 )
信号的数量较未裂阶段的数量有所下降, 但能量值 式中: B 为施荷应力水平等于 σ 时的衰减系数; d B
更大且相互接近。该阶段能量衰减系数骤降, 数量 为施荷应力水平从 σ 变化到 σ+dσ 时衰减系数的变
-7 -13 , 远小于未裂阶段的能量衰减系
级为 10 ~10 化量。
数。该阶段由于宏观裂纹不断扩展且向上延伸, 传感 fσ 可以用双曲函数表示, 即
()
器之间的信号传递存在阻碍, 声发射源信号难以在混 fσ = a / σ+ b ( 8 )
()
0
5
2023年 第45卷 第8期
无损检测