Page 39 - 无损检测2022年第十二期

周海鹏, 等:

基于非线性超声检测的搅拌摩擦焊接头疲劳寿命评价

; 。
0.6N 0 ⑤ 70% 寿命———疲劳次数 >0.6N 0
一般而言, 随机变量应服从正态分布, 但在样本
量较小的情形下, 可改用t 分布描述随机变量的分
, 则 P ( x|i )
布情况。疲劳阶段i 的样本数量为n i
可表示成自由度为 n i-1 的t 分布概率密度函数,
即 [ 12 ]
/
Γ ( n i 2 ) 1
P ( x| i ) = ×
Γ [( n i -1 )/ 2 ]
π ( n i -1 ) s i
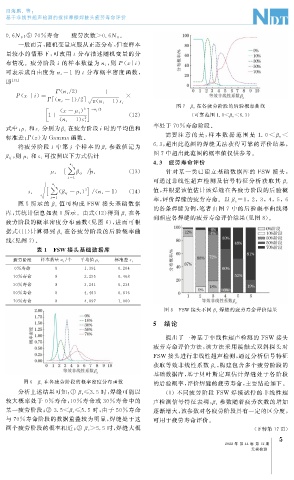
图 7 β e 在各疲劳阶段的后验概率曲线
)
i
( x - μ i - n / 2
1+ 2 ( 12 ) ( 可靠范围 1.0< β e<6.3 )
2
( n i -1 ) s i

分别为 在疲劳阶段 i 时的平均值和 率处于 70% 寿命阶段。
μ i β e
式中: 和 s i
需要注 意 的 是, 样 本 数 据 范 围 是 1.0< β e <
标准差; Γ ( z ) 为 Gamma函数。
将疲劳阶段i 中第 j 个样本的 参数值记为 6.3 , 超出此范围的焊缝无法获得可靠的评价结果,
β e
, 则 可按照以下方式估计 图 7 中超出此范围的概率值仅供参考。
β i j μ i 和 s i
n 4.3 疲劳寿命评价
i
μ i = / n i ( 13 ) 针对某一类已建立基础数据库的 FSW 接头,
∑ β i j
j=1
可通过非线性超声检测及信号特征分析获取其
n β e
i
2
(
s i = ∑ β i j - μ i ) /( n i -1 ) ( 14 ) 值, 并根据该值估计该焊缝在各疲劳阶段的后验概

j= 1 率, 评价焊缝的疲劳寿命。以
图 5 所示的 β e 值可构成 FSW 接头基 础数据 β e=1 , 2 , 3 , 4 , 5 , 6
库, 其统计信息如表 1 所示。由式( 12 ) 得到 在各 的各条焊缝为例, 笔者由图 7 中的后验概率曲线得
β e
到相应各焊缝的疲劳寿命评价结果( 见图 8 )。
疲劳阶段的概率密度分布函数( 见图 6 ), 进而可根
据式( 11 ) 计算得到 在各疲劳阶段的后验概率曲
β e
线( 见图 7 )。
表 1 FSW 接头基础数据库
疲劳阶段 样本数量n i / 个 平均值 μ i 标准差s i
0% 寿命 8 1.391 0.204
10% 寿命 8 2.255 0.468
30% 寿命 8 3.241 0.234
50% 寿命 8 4.463 0.616
70% 寿命 8 4.897 1.000
图 8 FSW 接头不同 β e 焊缝的疲劳寿命评价结果
5 结论
提出了一种基于非线性超声检测的 FSW 接头
疲劳寿命评价方法, 该方法采用接触式双斜探头对
FSW 接头进行非线性超声检测, 通过分析信号特征
获取等效非线性系数 , 构建包含多个疲劳阶段的
β e
基础数据库, 基于贝叶斯定理估计焊缝处于各阶段
图 6 β e 在各疲劳阶段的概率密度分布函数 的后验概率, 评价焊缝的疲劳寿命, 主要结论如下。

分析上述结果可知: ① β e≤3.5 时, 焊缝可能以 ( 1 )不同疲劳阶段 FSW 焊接试件的非线性超

较大概率处于 0% 寿命, 10% 寿命或 30% 寿命中的 声检测信号特征表明, 参数随着疲劳次数的增加
β e
某一疲劳阶段; ② 3.5< β e≤5.5 时, 由于 50% 寿命 逐渐增大, 该参数对各疲劳阶段具有一定的区分度,

与 70% 寿命阶段的数据重叠较为明显, 焊缝处于这 可用于疲劳寿命评价。

两个疲劳阶段的概率相近; ③ β e>5.5 时, 焊缝大概 ( 下转第 17 页)
5
2022 年 第 44 卷 第 12 期
无损检测