Page 82 - 无损检测2022年第九期

沈常宇,等:
承压类管道内壁损伤缺陷的低频电磁检测

个参数, 遗传算法重实数变量的可行域为[ 10 , 130 ],

-3
二进制编码的精度为 0.09634 。当阈值小于 10
时, 优化过程结束。达到该条件的遗传算法优化收

敛图如图 11 所示。由于适应度值达到 0.0000195
时满足收敛条件, 根据优化结果, 该系统的最佳磁芯

内径弧度为 220° , 磁芯厚度为 12mm 。
图 8 不同磁芯半径下磁感应强度的空间分布曲线
对磁芯厚度对传感器检测性能的影响进行了研

究。控制磁芯内径弧度为 220° , 半径为 45 mm 不

变, 磁芯厚度以 2mm 的步长在 4~12mm 间变化,
获得了其磁感应强度随磁芯厚度变化的分 布曲线
( 见图 9 )。由图 9 可以看出, 磁芯厚度从 4 mm 增

图 11 遗传算法优化收敛图
加到 12mm 的过程中, 磁感应强度也增大。
2.2 检测线圈优化
除了激励磁芯的优化设计, 检测线圈的优化设
计也是传感器优化的重要部分。根据法拉第电磁感
应定律, 对于一个匝数为 N 匝的线圈, 不考虑线圈
间存在间隙, 假设每匝穿过的磁通量相同, 则线圈的
感应电动势 E 为
dΦ di
E =-N =L ( 1 )
dt dt
图 9 磁感应强度随磁芯厚度变化的分布曲线 式中: dΦ / dt 为磁通量变化率; L 为电感系数, di / dt
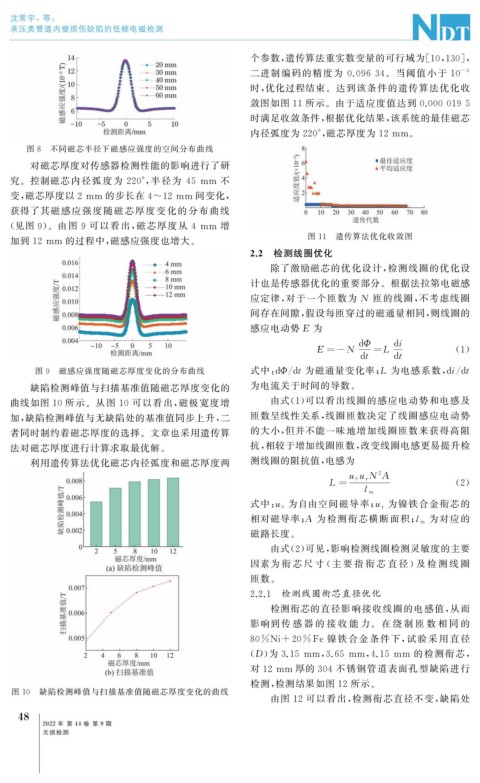
缺陷检测峰值与扫描基准值随磁芯厚度变化的 为电流关于时间的导数。
曲线如图 10 所示。从图 10 可以看出, 磁极宽度增 由式( 1 ) 可以看出线圈的感应电动势和电感及
加, 缺陷检测峰值与无缺陷处的基准值同步上升, 二 匝数呈线性关系, 线圈匝数决定了线圈感应电动势
者同时制约着磁芯厚度的选择。文章也采用遗传算 的大小, 但并不能一味地增加线圈匝数来获得高阻
法对磁芯厚度进行计算求取最优解。 抗, 相较于增加线圈匝数, 改变线圈电感更易提升检
利用遗传算法优化磁芯内径弧度和磁芯厚度两 测线圈的阻抗值, 电感为
2
u 0 u r N A
L = ( 2 )
l m
为镍铁合金衔芯的
式中: u 0 为自由空间磁导率; u r
为对应的
相对磁导率; A 为检测衔芯横断面积; l m
磁路长度。
由式( 2 ) 可见, 影响检测线圈检测灵敏度的主要
因素为 衔 芯 尺 寸 ( 主 要 指 衔 芯 直 径) 及 检 测 线 圈
匝数。
2.2.1 检测线圈衔芯直径优化
检测衔芯的直径影响接收线圈的电感值, 从而
影响到 传 感 器 的 接 收 能 力。 在 绕 制 匝 数 相 同 的
80%Ni+20%Fe 镍铁合金条件下, 试验 采 用 直 径

( D ) 为 3.15 mm , 3.65 mm , 4.15 mm 的检测衔芯,
对 12mm 厚的 304 不锈钢管道表面孔型缺陷进行

检测, 检测结果如图 12 所示。
图 10 缺陷检测峰值与扫描基准值随磁芯厚度变化的曲线
由图 12 可以看出, 检测衔芯直径不变, 缺陷处
4
8
2022 年 第 44 卷 第 9 期

无损检测