Page 36 - 无损检测2022年第九期

肖生玉,等:
裂缝深度检测的超声波首波相位反转机理分析

方法模拟了激光激发表面波与亚表面缺陷作用的传 L<L 0 时, 声波响应的首波为正波, 当 L>L 0 时, 首
播过程, 为亚表面缺陷的超声检测奠定了理论基础。 波由正波转变为负波( 见图2 ), 正负波相位相差 π , 在
上述提到的众多检测方法的应用场景仅局限于 临界点附近, 小范围挪动收发超声换能器便能捕捉到
实验室或 少 数 高 精 尖 工 况, 超 声 波 首 波 相 位 反 转 明显的相位反转现象。结合临界角δ 可评估裂缝深

法 [ 7-8 ] 凭借其准确、 简单、 易操作的优势, 收录于标准 度 H , H=L 0 2tan ( δ / 2 )]。压电超声换能器非对
/[·
CECS21 : 2000 《 超声法检测混凝土缺陷技术规程》 称布置[ 见图1 ( b )] 的情况下同样能捕捉到相位反转现

中, 并被广泛应用于建设工程质量检测领域。该方 象且临界角仍为δ , 相应的裂缝深度估算方法类似。
法早在 1982 年由童寿兴学者提出, 但其作用机理一
直未得到明确解释, 人们对首波相位反转的认识只
停留在其为一种试验现象的阶段, 因此有必要采用
理论分析、 有限元数值模拟与试验对比法对该问题
展开深入研究。
1 超声波首波相位反转法 图 2 首波波形的相位反转特征

针对实际工程结构中常见的混凝土表面垂直裂 2 理论分析
缝, 采用“ 一发一收” 方式将压电超声换能器对称布置
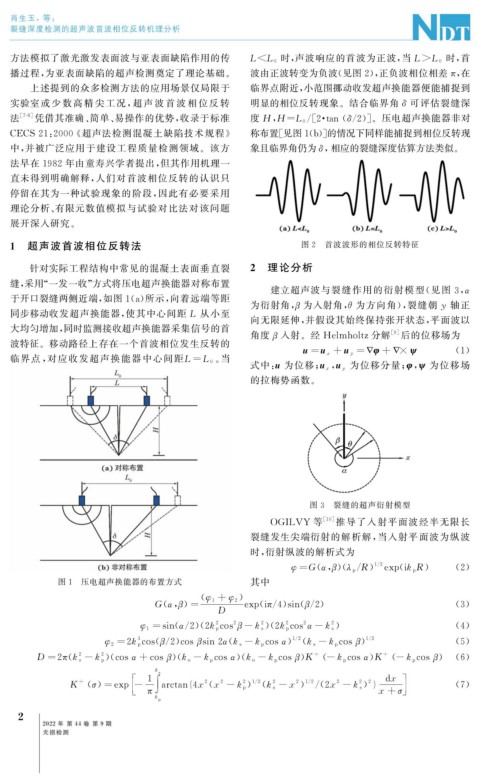
建立超声波与裂缝作用的衍射模型( 见图 3 , α
于开口裂缝两侧近端, 如图 1 ( a ) 所示, 向着远端等距
为衍射角, 为入射角, θ 为方向角), 裂缝朝 y 轴正
β
同步移动收发超声换能器, 使其中心间距 L 从小至
向无限延伸, 并假设其始终保持张开状态, 平面波以
大均匀增加, 同时监测接收超声换能器采集信号的首
角度 β 入射。经 Helmholtz分解 [ 9 ] 后的位移场为
波特征。移动路径上存在一个首波相位发生反转的
u= u x +u y = + ×ψ ( 1 )
φ
。 当
,
临界点, 对应收发超声换能器中心间距 L=L 0
φ ψ
式中: u 为位移; u x u y 为位移分量; , 为位移场
的拉梅势函数。

图 3 裂缝的超声衍射模型
OGILVY 等 [ 10 ] 推导了入射平面波经半无限长
裂缝发生尖端衍射的解析解, 当入射平面波为纵波
时, 衍射纵波的解析式为
(
φ =G ( α ,)( λ p R ) ex pik p R ) ( 2 )
/
1 / 2
β
图1 压电超声换能器的布置方式 其中
( )
(
G ( α ,) φ 1 + φ 2 ex piπ / 4 ) sin (/ 2 ) ( 3 )
β =
β
D
2 2 2 )( 2 2 2 ) ( 4 )
φ 1 = sin ( α / 2 )( 2k p cos β-k s 2k p cosα-k s

1 / 2
3 1 / 2 ) ( 5 )
β
φ 2 = 2k p cos (/ 2 ) cos β sin2α ( k s-k p cosα ) ( k s-k p cos β

2 2 )( )( ) + + ) ( 6 )
-
-
D = 2π ( k s -k p cosα+cos β k o-k p cosα )( k o-k p cos β K ( k p cosα ) K ( k p cos β
k
s
1

+
)
2
2 1 / 2
2 2
2
2
2 1 / 2
2
=
K ( σ ) ex p - arctan4 x ( x -k p ) ( k s -x ) /( 2 x -k s d x ( 7 )

π ∫ x + σ

k
p
2
2022 年 第 44 卷 第 9 期

无损检测