Page 84 - 无损检测2022年第三期

李 伟, 等:

储罐的不均匀沉降应力监测与检测技术

线性算法, 得出典型储罐在整体和局部差异沉降作 表 1 数值模拟参数
用下产生屈曲的规律; 此外, 罐体在局部差异沉降作 项目 参数 项目 参数
用下的行为与局部化程度有关。 FAN 等 [ 7 ] 实测了 储罐材料 Q345R 泊松比 μ =0.3
大型钢制储罐的沉降作用, 建立了基于泊松曲线的 弹性模量 / GPa 206 罐底厚度 / mm 4

沉降预测模型, 提出了预测储罐 屈曲行为的方法。 罐底内径 / mm 2.75 罐壁厚度 / mm 4
马云栋 [ 8 ] 通过 ABAQUS 软件进行数值分析, 研究 罐高 / m 1 满液位模拟水位 / m 0.72
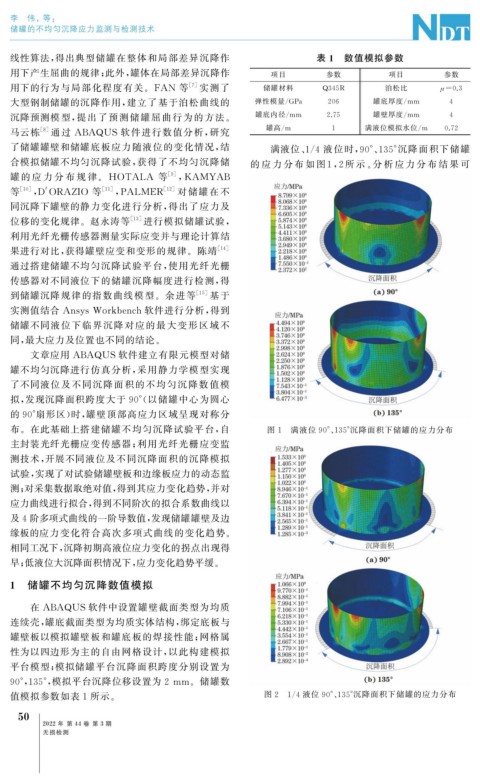
了储罐罐壁和储罐底板应力随液位的变化情况, 结 满液位、 1 / 4 液位时, 90° 、 135° 沉降面积下储罐
合模拟储罐不均匀沉降试验, 获得了不均匀沉降储 的 应 力 分 布 如 图 1 , 2 所 示 。 分 析 应 力 分 布 结 果 可
罐 的 应 力 分 布 规 律。 HOTALA 等 [ 9 ] , KAMYAB
等 [ 10 ] , D'ORAZIO 等 [ 11 ] , PALMER [ 12 ] 对 储 罐 在 不
同沉降下罐壁的静力变化进行分析, 得出了应力及
位移的变化规律。赵永涛等 [ 13 ] 进行模拟储罐试验,
利用光纤光栅传感器测量实际应变并与理论计算结
果进行对比, 获得罐壁应变和变形的规律。陈靖 [ 14 ]
通过搭建储罐不均匀沉降试验平台, 使用光纤光栅
传感器对不同液位下的储罐沉降幅度进行检测, 得
到储罐沉降规律的指数曲线模型。余进等 [ 15 ] 基于

实测值结合 Ans y sWorkbench 软件进行分析, 得到
储罐不同液位下临界沉降对应的最大变形 区域不
同, 最大应力及位置也不同的结论。
文章应用 ABAQUS 软件建立有限元模型对储
罐不均匀沉降进行仿真分析, 采用静力学模型实现
了不同液位及不同沉降面积的不均匀沉降 数值模
拟, 发现沉降面积跨度大于 90° ( 以储罐中心为圆心
的 90° 扇形区) 时, 罐壁顶部高应力区域呈现对称分
布。在此基础上搭建储罐不均匀沉降试验平台, 自 图 1 满液位 90° 、 135° 沉降面积下储罐的应力分布
主封装光纤光栅应变传感器; 利用光纤光栅应变监
测技术, 开展不同液位及不同沉降面积的沉降模拟
试验, 实现了对试验储罐壁板和边缘板应力的动态监
测; 对采集数据取绝对值, 得到其应力变化趋势, 并对
应力曲线进行拟合, 得到不同阶次的拟合系数曲线以
及4阶多项式曲线的一阶导数值, 发现储罐罐壁及边
缘板的应力变化符合高次多项式曲线的变化趋势。
相同工况下, 沉降初期高液位应力变化的拐点出现得
早; 低液位大沉降面积情况下, 应力变化趋势平缓。

1 储罐不均匀沉降数值模拟

在 ABAQUS 软件中设置罐壁截面类型为均质
连续壳, 罐底截面类型为均质实体结构, 绑定底板与
罐壁板以模拟罐壁板和罐底板的焊接性能; 网格属
性为以四边形为主的自由网格设计, 以此构建模拟
平台模型; 模拟储罐平台沉降面积跨度分别设置为
90° , 135° , 模拟平台沉降位移设置为 2mm 。储罐数

图 2 1 / 4 液位 90° 、 135° 沉降面积下储罐的应力分布
值模拟参数如表 1 所示。
0
5

2022 年 第 44 卷 第 3 期

无损检测